Chapter 2-3. 기초 시계열 분석
이번 장에서는 시계열 분석에서 자주 나오는 용어 및 알아야 할 개념들을 간단하게 정리해보고자 한다.
확률과정(Stochastic Process)
확률과정은 확률변수들의 수열이다. 즉, {Y(t), t = 0, ±1, ±2, ...} 형태로 나타낼 수 있으며, 시계열 데이터를 이해하려면 Y(t) 들의 결합 확률 분포를 분석해야 한다. 왜냐하면, 일반적인 시계열 데이터는 독립이 아니기 때문에, 결합 확률 분포를 각 확률 변수의 분포들로 분해할 수 없기 때문이다. 하지만, 평균과 분산을 분석하면 결합 확률 분포의 많은 부분을 이해할 수 있다.
평균, 분산, 공분산, 상관계수
앞서 Chapter 1. 기초 선형대수 및 통계학에서 간단하게 소개한 개념들을 수식으로 알아보자. 평균, 분산은 해당 시점의 확률 변수들의 평균, 분산이다.
$$\mu_{t} = E(Y_{t}), \,\,\, t = 0, ±1, ±2, ...$$ $$\sigma^{2}_{t} = Var(Y_{t}), \,\,\, t = 0, ±1, ±2, ...$$
그리고 공분산, 상관계수는 다른 시점의 확률변수들과의 관련성을 나타낸다.
$$\gamma_{t, s} = Cov(Y_{t}, Y_{s}), \,\,\, t, s = 0, ±1, ±2, ...$$ $$\rho_{t, s} = Cov(Y_{t}, Y_{s}), \,\,\, t, s = 0, ±1, ±2, ...$$
그리고 다음 두 가지 식은 시계열의 상관성을 분석할 때 자주 쓰이므로 잘 알아두자.
$$Cov \left (\sum_{i=1}^{m}C_{i}Y_{t_{i}}, \sum_{j=1}^{n}d_{j}Y_{s_{j}} \right ) = \sum_{i=1}^{m}\sum_{j=1}^{n}c_{i}d_{j}Cov(Y_{t_{i}}, Y_{s_{j}})$$ $$Var\left ( \sum_{i=1}^{n}C_{i}Y_{t_{i}} \right ) = \sum_{j=1}^{n}c^{2}_{i}Var(Y_{t_{i}}) + 2\sum_{i=2}^{n}\sum_{j=1}^{i-1}c_{i}c_{j}Cov(Y_{t_{i}}, Y_{s_{j}})$$
White Noise
백색 잡음 과정은 아무런 패턴 없이, 무작위적으로 진동하는 확률과정이다. 즉, 다음을 만족하는 확률과정이다. 개발한 모형이 제대로 모델링 했는 지 분석할 때, 잔차가 white noise를 따르는 지 확인해야 한다. 더 이상 모델에 추가해야 할 패턴이 데이터에 없다는 의미이기 때문이다.
$$ {e_{t}, \,\,\, t = 0, 1, 2, ...} \,\,\, where \,\,\, e_{t} \sim iid \,\,\, N(0, \sigma^2)$$
위의 식에서 iid란, identical and independent의 약어로 white noise끼리는 독립적이며(서로 선형/비선형적 관계가 없다) 서로 같은 분포를 따름을 의미한다.
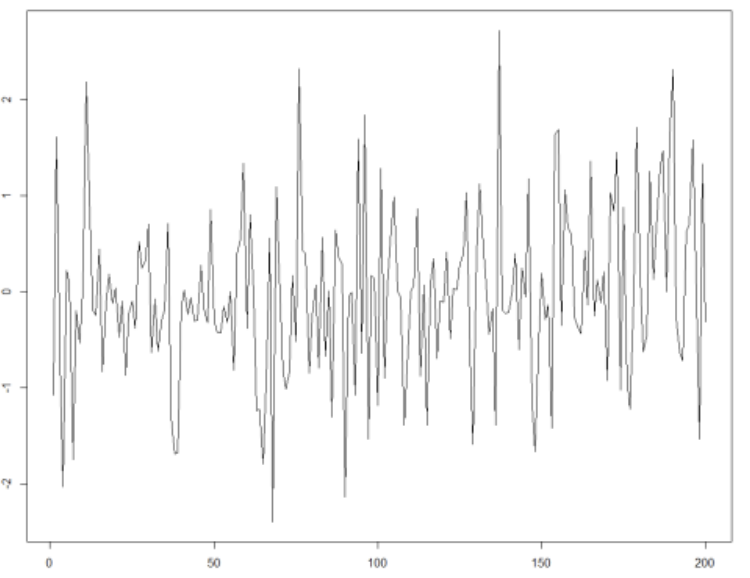
백색 잡음 과정의 평균, 분산, 공분산은 다음과 같다. 평균과 분산이 매 시점마다 일정하고, 공분산은 0임을 알 수 있다.
$$e_{t} = 0$$ $$\gamma_{t, x} = \sigma^2 \,\,\, if \,\,\, t = s \,\,\, else \,\,\, \gamma_{t, s} = 0$$ $$\rho_{t, s} = 1 \,\,\, if \,\,\, t = s \,\,\, else \,\,\, \rho_{t, s} = 0$$
실제로 그래프를 보더라도, 대부분의 데이터가 0 근처의 값을 갖는다. 분산도 일정해서 값이 변동하더라도 일정 값 안에서 진동한다.
Random Walk
Random Walk는 현 시점 데이터는 이전 시점 데이터에 현재 무작위 오차가 더해져서 생성됐다고 판단될 때 쓸 수 있는 확률 과정이다. 즉, 다음 두 식과 동일하다.
$$ Y_{t} = Y_{t-1} + e_{t} \,\,\, where \,\,\, e_{t} \sim iid \,\,\, N(0, \sigma^2) \,\,\, for \,\,\, all \,\,\, t = 0, 1, 2, ...$$ $$Y_{t} = \sum_{i = 1}^{t}e_{i}$$
Random Walk 과정의 평균, 분산, 공분산은 다음과 같다.
$$E(Y_{t}) = 0$$ $$\gamma_{t, s} = Cov\left ( \sum_{i = 1}^{t}e_{i} \sum_{j = 1}^{s}e_{j}\right ) = t\sigma^2, \,\, 1\leq t\leq s$$ $$\rho_{t, s} = \frac{t\sigma^2}{\sqrt{t\sigma^2}{\sqrt{t\sigma^2}}} = \sqrt{\frac{t}{s}}, \,\, 1\leq t \leq s$$
식을 해석해보면 평균은 0으로 일정하며, 분산은 시점 t가 커질수록 커진다. 그리고 시차가 작을수록 높은 선형 상관을 보이지만, 커질수록 상관은 낮아진다. 실제로 아래 그래프를 보면, 시점이 1000으로 갈수록 분산이 커져 평균인 0에서 멀어지는 것을 알 수 있다. 후에 배우겠지만, Random Walk는 비정상 시계열이다.

시계열 데이터의 특징
정상성(Stationarity)
정상성은 시계열 분석에서 핵심적인 개념이다. 데이터가 정상성을 만족하지 않으면, 시계열은 비정상 시계열(Non-Stationary Time Series)이 되며 시계열 분석을 수행할 수 없다. 정상성을 만족하지 않는 데이터는 정상성을 만족하도록 전처리를 해야 분석을 수행할 수 있다. 정상성의 개념은 크게 두 가지가 있다. 첫 번째는 Strict Stationarity이다. Strict Stationarity의 정의는 다음과 같다.
$$ \Pi(Y_{t_{1}}, Y_{t_{2}}, ..., Y_{t_{n-1}}, Y_{t_{n}}) = \Pi(Y_{t_{1-k}}, Y_{t_{2-k}}, ..., Y_{t_{n-1-k}}, Y_{t_{n-k}}) $$
시차 k 및 시점\(t_{1}, t_{2}, ..., t_{n}\)을 어떻게 선택하더라도 결합 확률 분포 가 항상 일정해야 한다는 뜻이다. 그래야 관측된 부분 시계열만을 이용해서 전체 확률 과정에 대한 추론을 할 수 있기 때문이다. 하지만, strict stationarity를 보이는 것이 쉽지 않으므로 이와 비슷하지만 수학적으로 약화된 weak stationarity 가정이 생겼다. Weak stationarity는 다음 두 조건을 만족하면 성립한다.
$$\mu_{t} = c \,\,\, for \,\,\, all \,\,\, time \,\,\, t$$
$$\gamma_{t, t-k} = \gamma_{0, k} \,\,\, for \,\,\, all \,\,\, time \,\,\, t, k$$
평균이 일정하고, 공분산이 시차에만 의존하면 weak stationarity 시계열이다. 일반적으로 말하는 stationarity는 weak stationarity를 의미한다. 대표적인 정상 시계열은 백색 잡음 과정이다.
트렌드와 계절성, 주기
트렌드는 시계열이 단/장기적으로 보이는 추세를 의미하며, 계절성은 일정한 빈도를 가지며 반복적으로 나타나는 패턴을 의미한다. 반면, 주기는 일정한 빈도를 가지지 않고 반복적으로 나타나는 패턴을 의미한다. 아이스크림 판매량 같은 경우는 일반적으로 여름에 높고 겨울에 낮을 것이므로 1년 간격의 계절성으로 볼 수 있다. 반면, 경기 순환은 반복되지만 호황과 불황이 일정한 간격을 가지지 않아서 주기로 볼 수 있다. 시계열은 트렌드, 계절성, 주기 그리고 Random Noise의 합으로 보거나 각각으로 분해할 수 있다.
$$ Y(t) = T(t) + S(t) + C(t) + e_{t}$$
XAIOps 의 장기 부하 예측 모델들은 하나의 단일 모형을 쓰지 않고, 시계열을 각각의 성분으로 분해한 다음 각 성분별로 모형을 만들어서 예측 후 다시 종합하는 방식을 사용하고 있다. 각 성분을 예측할 때 회귀 분석 혹은 시계열 모형들을 활용해서 진행해도 된다.
정상 시계열(Stationary Time Series)
이동 평균 과정(Moving Average Process)
현재의 오차가 과거 오차들과 상관된다면, 아래와 같은 이동 평균 과정으로 모형화 할 수 있다.
$$ Y_{t} = e_{t} - \Theta_{1}e_{t-1} - \Theta_{2}e_{t-2} - ... - \Theta_{t-q}e_{t-q}$$
q 가 1, 2 그리고 일반화된 k 일 때 어떤 특징을 가지는지 알아보자.
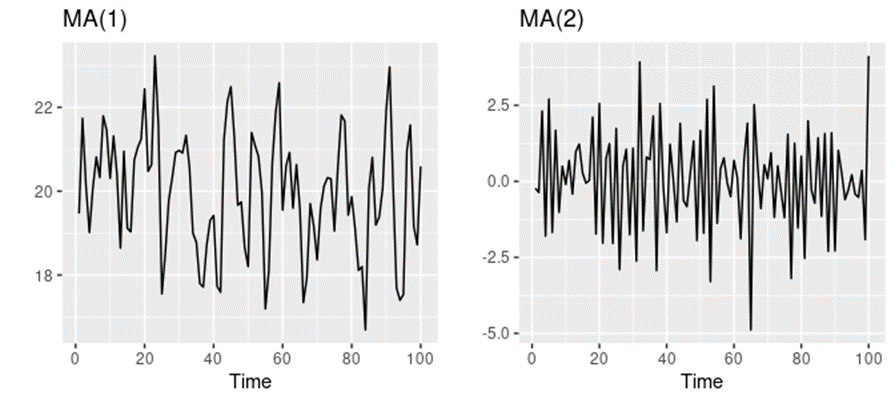
q = 1 이면 로 모델링 할 수 있고, MA(1) 확률 과정의 특징은 다음과 같다. 여기서 공분산, 상관계수는 k = 1 인 경우에만 성립하며, 그 외의 경우에는 전부 0이다.
$$E(Y_{t}) = 0$$ $$Var(Y_{t}) = (1 + \Theta^2)\sigma^2$$ $$Cov(Y_{t}, Y_{t-1}) = -\Theta\sigma^2$$ $$Cor(Y_{t}, Y_{t-1}) = \frac{-\Theta\sigma^2}{(1+\Theta^2)\sigma^2} = \frac{-\Theta}{(1+\Theta^2)}$$
1차 이동 평균 과정은 평균이 0으로 일정하며, 공분산이 시점에 따라 달라지지 않으므로 정상 확률 과정이다. 그리고 시차가 1인 경우에는 선형 상관이 있고 그 이후부터는 없다. \(p_{k} = 0, \, k \leq 2\) 평균이 0인 이유는 확률 변수 \(Y_{t}\)는 확률 과정 {\(Y_{t}\)} 평균을 뺀 값으로 가정하기 때문이다.
q = 2 이면 \(Y_{t} = e_{t} - \Theta e_{t-1} - \Theta e_{t-2}\) 로 모델링 할 수 있고, 확률 과정의 특징은 다음과 같다.
$$ E(Y_{t}) = 0$$ $$Var(T_{t}) = (1 + \Theta_{1}^2 + \Theta_{2}^2)\sigma^2$$ $$Cov(Y_{t}, Y_{t-2}) = Cov(e_{t} - \Theta_{1}e_{t-1} - \Theta_{2}e_{t-2},e_{t-1} - \Theta_{1}e_{t-2} - \Theta_{2}e_{t-3}) = (-\Theta_{1} + \Theta_{2}\Theta{1})\sigma^2$$ $$Cov(Y_{t}, Y_{t-2}) = Cov(e_{t} - \Theta_{1}e_{t-1} - \Theta_{2}e_{t-2}, e_{t-2} - \Theta_{1}e_{t-3} - \Theta_{2}e_{t-4}) = -\Theta_{2}\sigma^2$$ $$Corr(Y_{t}, Y_{t-1}) = \frac{(-\Theta_{1} + \Theta_{2}\Theta_{1})}{(1 + \Theta_{1}^2 + \Theta_{2}^2)}$$ $$Corr(Y_{t}, Y_{t-2}) = \frac{-\Theta_{2}}{(1 + \Theta_{1}^2 + \Theta_{2}^2)}$$
2차 이동 평균 과정 MA(2) 도 평균이 0으로 일정하며, 공분산이 시점에 의존하지 않기 때문에 정상 확률 과정이다. 다만, 이전과 달리 시차가 2 인 경우에도 선형 상관이 있고 그 이후부터는 없다.
q = k 인 경우를 추측해보자. 평균이 0, 공분산은 시점에 의존하지 않으므로 정상 확률 과정일 것이다. 그리고 시차가 k 인 경우까지는 선형 상관이 있고, k 이후부터는 없을 것으로 추측할 수 있다. q = k 인 MA(K) 확률 과정의 특징은 다음과 같다. 증명은 위의 방식과 동일하게 진행하면 된다.
$$E(Y_{t}) = 0$$ $$Var(Y_{t}) = (1 + \Theta_{1}^2 + \Theta_{2}^2 + .. + \Theta_{k}^2)\sigma^2$$ $$\rho_{k} = \frac{-\Theta_{k} + \Theta_{1}\Theta_{k+1} + \Theta_{2}\Theta_{k+2} + ... + \Theta_{q}\Theta_{k+q}}{(1 + \Theta_{1}^2 + \Theta_{2}^2 + ... + \Theta_{k}^2)} \,\,\, for \,\,\, k = 1, 2, 3, ..., q$$
자기 회귀 과정(Auto Regressive Process)
자기 회귀 과정은 현재 값이 과거 p 시점 이전의 데이터들의 영향을 받는다고 판단될 때 사용할 수 있다. 수식으로 표현하면 다음과 같다.
$$Y_{t} = \phi_{1}Y_{t-1} + \phi_{2}Y_{t-2} + ... + \phi_{p}Y_{t-p} + e_{t}$$
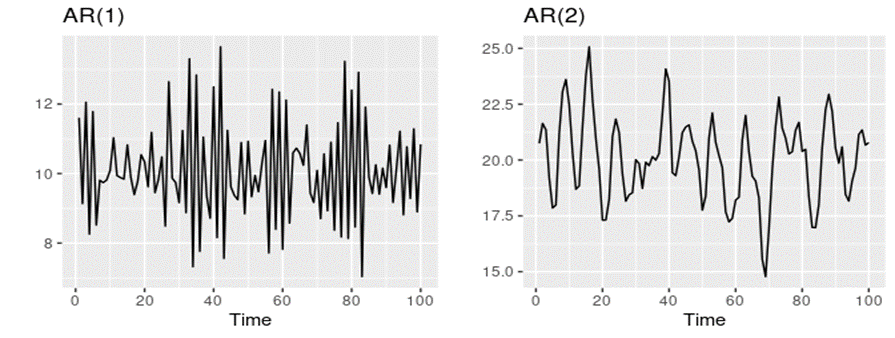
1차 자기 회귀 과정을 살펴보자. 는 백색 잡음 과정이며, 현 시점의 오차는 과거 데이터와 독립이라고 가정한다. p = 1 인 경우는 다음과 같다.
$$Y_{t} = \phi(Y_{t-1}) + e_{t}$$
AR(1) 확률 과정의 특징은 다음과 같다.
$$E(Y_{t}) = 0$$ $$Var(Y_{t}) = \frac{\sigma^2}{1 - \phi^2}$$ $$\gamma_{k} = \phi^{k}\gamma_{0} = \phi^{k} \frac{\sigma^2}{1 - \phi^2} \,\, (\because \gamma_{k} = \phi\gamma_{k-1})$$ $$\rho_{k} = \phi^{k}$$
이동 평균 과정과 달리 자기 회귀 과정에서는 시차가 1보다 커져도 자기 상관이 있는 것을 알 수 있다. 그리고 이동 평균 과정과 달리 자기 회귀 과정은 특정 조건을 만족해야 정상성을 만족한다. 식을 재귀적으로 무한히 쓰면, 현재 값은 과거 시점의 오차들의 가중합이다.
$$Y_{t} = e_{t} + \Phi e_{t-1} + \Phi^2 e_{t-2} + ...$$
위의 식은 선형 확률 과정(General Linear Process)이며, \(\sum_{j=1}^{\infty}\Phi^{2j}\) 가 수렴해야 정상 확률 과정이 된다는 것이 알려져 있다. 이 식을 만족하는 범위는 \(-1 \leq \phi \leq 1\) 이다. 그렇지 않으면, 가장 최근 데이터보다 더 과거 시점 데이터의 가중치가 커서 논리적으로 타당하지 않은 모형이 되기 때문이다.
AR(2)인 경우에는 \(-1 \leq \phi_{2} \leq 1, -1 \leq \phi_{1} + \phi_{2} \leq 1, -1 \leq \phi_{2} - \phi_{1} \leq 1\) 이라는 세 가지 식을 모두 만족해야 정상 시계열이 되며, 3차 이상은 복잡해서 생략한다.
AR 모형 같은 경우는 과거 시점의 값들이 현재 시점에 연쇄적으로 영향을 주기 때문에, 특정 시점 값끼리 상관을 측정하려면 중간 시점의 영향력을 제거하고 비교해야 한다. 이를 측정한 함수가 부분 자기 상관 함수이다. 부분 자기 상관 함수 \(\phi_{kk}\)는 다음과 같다.
$$\phi_{kk} = cor(Y_{t}, Y_{t-k} | Y_{t-1}, Y_{t-2}, ..., Y_{t-k+1})$$
즉, 중간 시점의 값들은 주어진 값으로 보고 \(Y_{t}\) 와 \(Y_{t-k}\) 사이의 변동성만 계산한 것이다. \(\phi_{kk}\)를 계산하는 구체적으로 계산하는 방법은 다음과 같다.
$$\phi_{kk} = cor(Y_{t} - \beta_{1}Y_{t-1} - \beta_{2}Y_{t-2} - ... - \beta_{k-1}Y_{t-k+1}, Y_{t-k} - \beta_{1}Y_{t-k+1} - \beta_{2}Y_{t-k+2} - ... - \beta_{k-1}Y_{t-1})$$
선형 회귀 분석을 이용해서 Y_t 에 영향을 주는 \(Y_{t-1},Y_{t-2}, ... ,Y_{t-k+1}\)의 영향력을 제거하고 \(Y_{t-k}\) 가 \(Y_{t-1},Y_{t-2}, ... , Y_{t-k+1}\)에 끼친 영향력을 제거한 다음에 구한 \(Y_{t}\) 와 \(Y_{t-k}\) 의 상관이다. AR(1)모형과 MA(1) 모형의 부분자기상관함수는 각각 다음과 같다. \(\phi_{11} = 1\)로 가정한다.
$$\phi_{00} = 0 \,\,\, for \,\,\, k > 1$$ $$\phi_{kk} = - \frac{\Theta^{k}(1-\Theta^2)}{1 - \Theta^{2(k+1)}} \,\,\, for \,\,\, k \geq 1$$
자기 상관 함수는 AR 모형이 조금씩 줄어들고, MA 모형은 q 시차가 지나면 전부 0 이었다. 반대로 부분 자기 상관 함수는 AR 모형이 p 시차가 지나면 전부 0이지만, MA 모형은 조금씩 줄어든다.
가역성(invertibility)
AR 모형은 MA 모형의 차수를 무한하게 늘린 확률 과정으로 볼 수 있다. 역으로 MA 모형도 AR 모형 형태로 나타낼 수 있으면, MA 모형이 가역적이다고 말한다. \(e_{t} = Y_{t} + \Theta(e_{t-1})\)을 재귀적으로 쓰면, 다음과 같아진다.
$$E_{t} = Y_{t} + \Theta(Y_{t-1}) + \Theta^2Y_{t-2} + ... $$
AR 형태로 풀면, 다음과 같다.
$$ Y_{t} = -(\Theta(Y_{t-1} + \Theta^2(Y_{t-2} + ...) + e_{t}$$
가역성을 만족하려면, -1 < \(\Theta\) < 1 이어야 한다. 그렇지 않으면, 가장 최근 관측값이 더 과거 관측값보다 더 작은 가중치를 갖게 되기 때문이다.
자기 회귀 이동 평균(Auto Regressive Moving Average) 과정
자기 회귀 이동 평균 과정은 자기 회귀 과정과 이동 평균 과정의 조합으로 데이터를 설명하는 것이다. 각 과정의 차수에 따라서 ARMA(p, q) 라고 표현한다. ARMA(1, 1) 과정은 다음과 같다.
$$Y_{t} = \phi(Y_{t-1}) + e_{t} - \Theta(e_{t-1})$$
ARMA(1, 1)의 자기 상관 함수는 ϕ,θ에 의존하며 AR처럼 ϕ 에 따라 점차 감소하는 것을 알 수 있으며, 정상성을 만족하는 조건은 -1 < \(\phi\) < 1 이다.
$$ \rho_{k} = \frac{(1-\phi\Theta)(\phi - \Theta)}{1 - 2\Theta\phi + \Theta^2}\phi^{k-1} \,\, (k \geq 1)$$
ARMA(p, q) 는 일반적으로 정상성과 가역성을 만족시켜야 한다.
비정상(Non-Stationarity) 시계열
시계열 데이터가 항상 정상성을 만족할 수는 없다. 비정상 시계열은 어떤 특징을 가지며, 어떻게 전처리하고 모델링하는지 알아보자.
AR(1) 과정에서 정상성을 만족하려면, -1 < ϕ < 1이어야 한다. 이를 만족하지 않는 경우 어떻게 되는지 확인해보자. 비정상 AR(1) 과정인 \(Y_{t} = 3Y_{t-1} + e_{t}\) 을 생각해보자. 식을 재귀적으로 풀어보면, 다음과 같아진다. $$ Y_{t} = e_{t} + 3e_{t-1} + 3^2(e_{t-2}) + ... + 3^{t-1}(e_{1}) + e^t(Y_{0})$$
현재 값은 과거 오차들의 가중 합이지만, 더 과거 시점의 오차가 현재 값에 더 큰 영향을 주면서 시계열은 발산하게 된다. \(Y_{t}\) 의 특성은 다음과 같다. \(Y_{0} = 0\) 이라고 가정하자. $$Var(Y_{t}) = \sigma^2(\frac{9^{t}-1}{8})$$ $$Cov(Y_{t}, Y_{t-k}) = 3^{k}\sigma^{2}(\frac{9^{t-k} - 1}{8})$$ $$Cor(Y_{t}, Y_{t-k} = 3^{k}\sqrt{\frac{9^{t-k} - 1}{9^{t} - 1}}$$ 시간이 지날수록 분산이 점점 커지는 것을 알 수 있으며, k가 어느 정도 커져도 자기상관이 1에 가까운 값임을 알 수 있다. 만약 \(\phi = 1\)이면, 이미 언급한 Random Walk 과정이 된다.
차분(Differencing)
차분은 비정상 시계열을 정상 시계열로 만드는 방법 중 하나이다. 시계열이 \(Y_{t} = M_{t} + e_{t} \,\,\, where \,\,\, M_{t} = M_{t-1}+ \varepsilon_{t}\) 형태로 이루어졌다고 하자. \(Y_{t}\) 는 Random Walk \(M_{t}\) 에 영향을 받는 비정상 시계열이다. 1차 차분한 시계열 \(∇ Y_{t}\)는 다음과 같다.
$$Y_{t} - Y_{t-1} = ∇Y_{t} = M_{t} - M_{t-1} + e_{t} - e_{t-1}$$ $$∇Y_{t} = \varepsilon_{t} + e_{t} - e_{t-1}$$
시계열 \(∇Y_{t}\) 의 Auto Correlation 은 \(-\frac{1}{2 + (\sigma^{2}_{\varepsilon}/\sigma^{2}_{e})}\) 로 계산된다. 상관이 시점에 의존하지 않으므로, 차분하면 정상 시계열이 되는 것을 알 수 있다.
과대 차분(Over-differencing)
차분을 하면 정상 시계열로 만들 수 있지만, 필요 이상의 차분을 하게 되면 모형에 문제를 일으키게 된다. Random Walk 모델 \(Y_{t} = Y_{t-1} + e_{t}\) 를 생각해보자.
Random Walk 모델을 1차 차분한 \(∇Y_{t}\) 는 white noise 가 되어 정상 시계열이다. Random Walk 를 2차 차분하면 \(∇^2 (Y_{t}) = e_{t}- e_{t-1}\) 형태의 1차 이동 평균 과정이 된다. 1차 차분으로 정상성을 이미 만족시켰으므로, 굳이 차분을 한 번 더 할 필요가 없다. 2차 차분을 하면 오히려 불필요한 이동 평균 모형의 모수를 추정해야 하며, 이동 평균 모형의 가역성이 깨질 수도 있다. 차분은 보통 1회, 최대 2회 정도면 충분하다.
자기 회귀 누적 이동 평균(ARIMA) 모형
d번 차분한 시계열이 ARMA(p, q)를 따르게 되면, 원 시계열은 ARMA(p, d, q)를 따르게 된다.
\(∇^{d}Y_{t} = \phi_{1}∇^{d}Y_{t-1} + \phi_{2}∇^{d}Y_{t-2} + ... + \phi_{p}∇^{d}Y_{t-p} + e_{t} - \Theta_{1}e_{t-1} - ... - \Theta_{q}e_{t-q}\) 로 쓸 수 있다.
예측(Forecasting)
현재 시점 t로부터 p시점 뒤의 예측값 \(\hat{Y_{t}}\) (p) 는 다음처럼 정의할 수 있다.
$$\hat{Y_{t}}(p) = E(Y_{t+p}|Y_{1}, Y_{2}, ..., Y_{t})$$
조건부 기댓값을 쓰는 이유는 수학적으로 예측 오차를 가장 최소화하기 때문이다. 확률 과정은 다양한 경로를 보일 수 있는데, 과거 값은 여러 경로 중 하나가 실현된 것이므로 그 자체에 정보가 있다고 볼 수 있다. 이 정보를 사용해서 미래를 예측하는 것이 직관적으로도 타당하다. 재귀적으로 예측값을 구해서 목표 시점의 예측값을 계산한다.
AR(1)
이제부터 \(Y_{t}\)의 평균이 0이 아니라고 가정하자. 그렇다면, \(Y_{t}\)를 쓰면 다음과 같아진다. 위에서 소개한 AR(1) 과정의 평균은 0으로 가정했기 때문이다.
$$Y_{t} - \mu = \phi(Y_{t-1} - \mu) + e_{t}$$
\(Y_{t+1}\)을 예측해야 하므로, 식을 \(Y_{t+1} - \mu = \phi(Y_{t} - \mu) + e_{t+1}\) 로 쓸 수 있다. 조건부 기댓값을 구하면 다음과 같다. \(Y_{t}\) 가 주어졌기 때문에, 중간의 조건부 기댓값은 상수가 되고 미래의 오차는 과거 값과 독립이라고 가정했기 때문이다.
$$E(Y_{t+1} | Y_{t}, Y_{t-1}, ..., Y_{1}) - \mu = \phi(E(Y_{t}|Y_{t}, Y_{t-1}, ..., Y_{1}) - \mu) + E(e_{t+1}|Y_{t}, Y_{t-1}, ... Y_{1})$$ $$\hat{Y_{t}}(1) - \mu = \phi(Y_{t} - \mu) + E(e_{t+1})$$ $$\hat{Y_{t}}(1) = \phi(Y_{t} - \mu) + \mu$$
일반화하면, \(\hat{Y_{t}}(p) = \mu + \phi(\hat{Y_{t}}(p-1) - \mu)\)이 된다. 재귀적으로 계산하면, \(\hat{Y_{t}}(p)\) 는 다음과 같다.
$$\hat{Y_{t}}(p) = \mu + \phi^{p}(Y_{t} - \mu)$$
AR(1)의 stationary condition 은 -1 < \(\phi\) < 1 이므로, AR(1)의 예측값은 장기적으로 평균에 수렴하게 되는 것을 알 수 있다.
MA(1)
\({Y_{t}}\) 가 이동 평균 과정이라면, 다음과 같다. $$Y_{t} = \mu + e_{t} - \Theta(e_{t-1})$$ \(\hat{Y_{t}}(1)\)을 구해보자. $$Y_{t+1} = \mu + e_{t+1} - \Theta(e_{t})$$ $$E(Y_{t+1} | Y_{t}, Y_{t-1}, ..., Y_{1}) = \mu + E(e_{t+1} | Y_{t}, Y_{t-1}, ..., Y_{1}) - \Theta(E(e_{t} | Y_{t}, Y_{t-1}, ..., Y_{1}))$$
만약 이동 평균 과정이 가역적이라면, \(e_{t}\)는 \(Y_{t},Y_{t-1}, ..., Y_{1}\) 들로 표현되므로 상수처럼 취급된다. 따라서, \(\hat{Y_{t}}(1)\)은 다음과 같다. $$\hat{Y_{t}}(1) = \mu - \Theta(e_{t})$$ \(\hat{Y_{t}}(p)\)를 구해보자. $$Y_{t+p} = \mu + e_{t+p} - \Theta(e_{t+p-1})$$ $$E(Y_{t+p} | Y_{t}, Y_{t-1}, ..., Y_{1}) = \mu + E(e_{t+p} | Y_{t}, Y_{t-1}, ..., Y_{1}) - \Theta(E(e_{t+p-1} | Y_{t}, Y_{t-1}, ..., Y_{1}))$$ $$\hat{Y+{t}}(o) = \mu + E(e_{t+p}) - \Theta(E(e_{t+p-1}) = \mu$$
이동 평균 과정은 p가 1보다 크면, 예측값은 항상 평균값이 된다.
ARMA(p, q)
ARMA(p,q) 모형은 장기적으로는 확률 과정의 평균 \(\mu\)로 수렴하게 된다. 이외에도 계절성을 반영한 모형, 조건부 이분산 모형 등 다양한 모형들이 있다. 해당 모형들이 포착하려고 하는 패턴을 이해할 때 위의 지식들이 기본 구성 요소가 되므로 숙지하면 좋다.
다음 챕터부터는 본격적으로 머신러닝(Machine Learning)이 무엇인지 공부해 볼 것이다. 머신러닝의 정의에 대해 알아보고, 여러 알고리즘의 훈련과정을 공부하고 실습을 해보자.

글 | AI 그룹 김경준
'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 3-2. 모델 훈련 (0) | 2023.01.19 |
|---|---|
| Chapter 3. 머신러닝 (0) | 2022.11.23 |
| Chapter 2-2. 시계열 데이터 전처리 (0) | 2022.09.28 |
| Chapter 2. Pandas 3편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.08.25 |
| Chapter 2. Pandas 2편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.08.25 |





댓글