Chapter 3-6. 차원 축소
머신러닝에 대해 공부하다 보면 차원의 저주 (Curse of Dimension) 라는 이야기를 종종 보게 될 것이다.
본 챕터에서는 "차원의 저주" 란 무엇인지 설명하고, 이 문제를 해결하기 위한 차원 축소 기법에 대해서 알아보도록 하자.
차원의 저주 (Curse of Dimension)
현실 세계에서 우리가 다루게 될 데이터는 굉장히 다양하고 많은 특성들을 가지고 있다.
예를 들어, "영화"라는 데이터를 예시로 설명하자면, "영화"라는 데이터를 나타내기 위한 특성으로는 영화의 제목, 개봉 시기, 장르, 감독, 배우, 예산, 시리즈 유무, 평점, 누적 관객 수, 수익 등 수 많은 특성들이 존재한다.
데이터 특성의 수가 많다라는 것은 머신러닝 학습 시 훈련 시간의 증가와 좋지 못한 성능을 초래하게 된다.
그 이유는 데이터 특성(Feature)을 머신러닝에서는 좌표 공간을 통해 표현하기 때문인데 예를 들어 영화 데이터 중 "영화 수익" 이라는 특성(Feature)은 수학적인 공간에서 X 라는 축으로 표현될 수 있으며 "누적 관객수" 라는 특성(Feature)은 또 다른 좌표 축인 Y 로 표현될 수 있다.
이렇듯 특성(Feature)이 증가할수록 머신러닝의 수학적 공간인 차원도 증가하게 되는데 차원이 증가할수록 데이터 사이의 공간은 지수적으로 증가하게 된다. 특정 실제 값을 표현하기 위해서 값이 존재하지 않는 빈 공간이 많아 진다는 의미이다.
인공지능 개념에서 이를 보통 "Sparse한 상태" 라고 표현한다.
결국 높은 차원을 가지는 데이터의 경우, 전체 데이터에서 실제 값을 가지는 데이터보다 데이터가 없는 상태인 '0' 값으로 (빈 공간) 대부분으로 구성되게 된다.

| 문제점 1 | 학습 훈련 시간의 증가 |
| 문제점 2 | Sparse 한 공간으로 인해 연산에서 성능 저하 |
위와 같이 차원이 커지며 발생하는 문제점들을 해결하는 방법 중 가장 명확한 이론적인 방법은 증가된 차원 공간 크기에 맞춰 실제 값을 가지는 데이터 표본의 양을 아주 크게 늘리는 것이다. (이는 Sparse 한 공간을 실 데이터로 채우는 것)
하지만 우리가 다루는 현실 세계에서의 데이터를 지수적으로 증가하는 차원 공간에 맞춰 늘리는 일은 어려우며 사실상 불가능하다.
그래서 우리는 수 많은 특성(차원) 중 데이터의 의미를 잘 표현하고 대표할 수 있는 특성을 찾아 불필요한 특성을 제거하거나 병합하는 방법들을 사용하며 원론적으로 "차원을 축소하는" 방식을 통해 위 문제를 해결하고자 한다.
차원 축소
일반적으로 차원 축소의 기법은 여러 차원 중 하나의 차원(수학적 관점에서 축)을 제거하여 차원을 감소시키는 방법이다. 이러한 방법에 대표적으로 널리 알려져 있는 차원 축소의 한 방법인 "주성분 분석(PCA)" 알고리즘에 대해 알아보자.
주성분 분석(PCA)
주성분 분석이란, 데이터를 하나의 축으로 '투영'시키는 것이다. 투영(projection) 이란 통상적으로 n 차원에서 n-1 차원으로 좌표를 변환시키는 것을 의미한다. 데이터가 투영된 하나의 축 자체를 주성분이라고 이야기하며 주성분 축의 선택 기준은 데이터를 투영했을 때 가장 높은 분산을 가지는 축이 기준이 된다.
그 이유에 대해 설명하자면 분산이 작은 경우에는 데이터의 정보 손실이 크기 때문이다. 예를 들어 위에서 언급한 "영화" 데이터에는 10개의 특성(Feature)이 있다. 주성분 축을 찾는 일은 10개의 특성을 가진 전체 데이터 분포에서 주요한 성분이 되는 (대표가 되는) 특성을 찾는 일인데, 분산이 작은 축을 주성분 축으로 선택하게되면 10개의 특성 정보를 반영하기에 어렵다. 성격이 다른 데이터의 경우에도 같은 위치에 중복으로 또는 가까운 거리에 오밀조밀하게 위치하게 될 것이다. 이렇게 된다면 10개의 특성 정보에서 손실이 발생하게 되는 것이다.
하지만 반대로 분산이 큰 축(특성) 을 선택하게 되었을 때, 데이터를 표현할 수 있는 범위가 넓어지게됨으로 10개의 특성 정보를 적절히 표현할 수 있게될 것이다. 따라서 주성분 분석에서는 차원을 줄이는 과정에서 발생되는 데이터 정보 손실을 최소화하는 방향으로 가장 큰 분산을 가지는 축을 주성분으로 사용하게 된다.
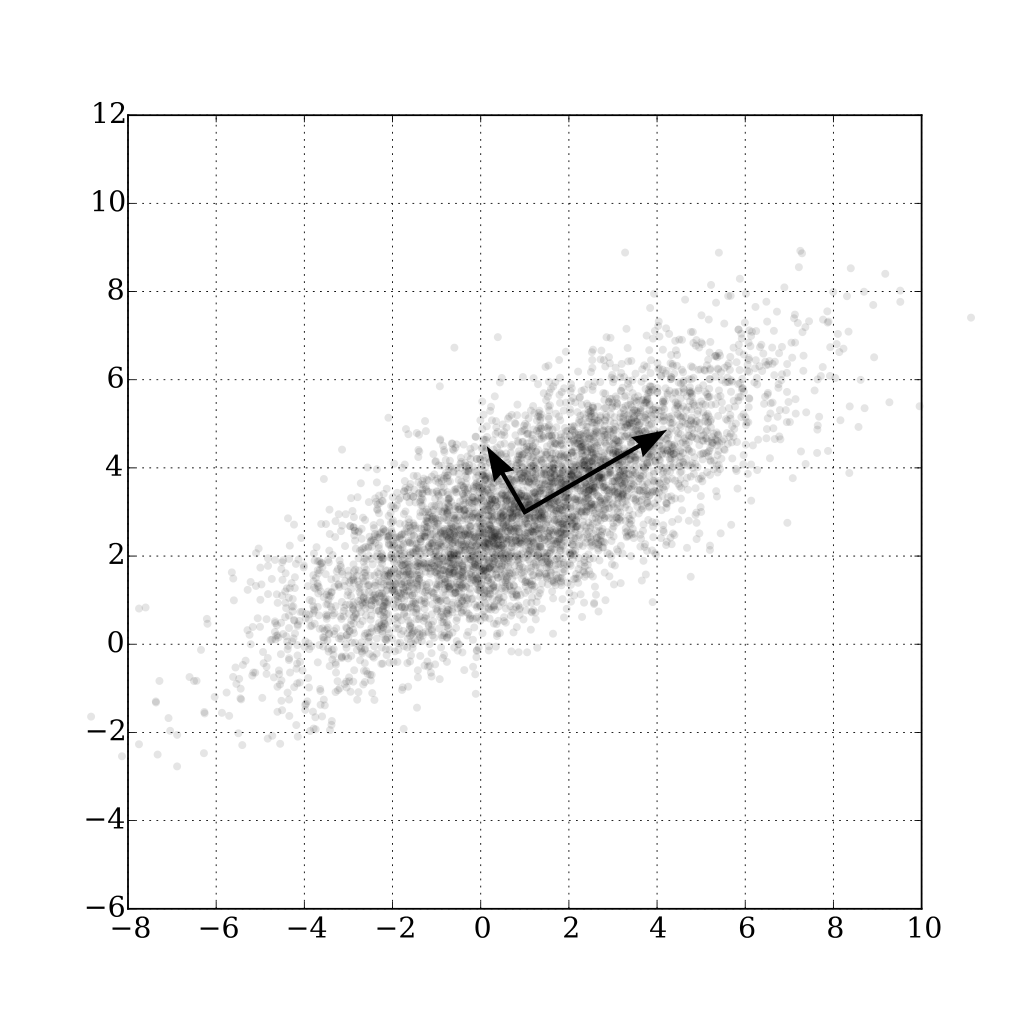
위 그림을 해석하자면 데이터 분포 속에 두 개의 축을 확인할 수 있다. 1시 방향으로 길게 뻗은 축을 'm' 이라하고, 11시 방향으로 짧게 뻗은 축을 'n' 이라고 하겠다. 축을 기준으로 데이터를 투영(Projection)하였을 때 모습은 다음과 같다.

넓게 퍼져있는 데이터 분포를 하나의 축으로 투영시키는데 'n' 축을 기준으로 투영했을 때는 데이터의 분산이 작아 좁은 범위를 가지게 될 것이고, 'm' 축을 기준으로 투영했을 때는 분산이 크기때문에 넓은 범위를 가지게될 것이다.
따라서 PCA는 다음과 같은 프로세스로 동작한다.
1. 데이터 공간에서 가장 큰 분산을 가지는 축을 생성한다.
2. 최초 생성된 축과 직교의 벡터 방향으로 똑같이 분산을 최대로 보존하는 두 번째 축을 생성한다.
3. 고차원의 경우 위와 같은 방식에 이어 세 번째 축, 네 번째 축 ... i 번째 까지 반복하며, 주성분 축을 찾는다.
원본 데이터는 이렇게 생성된 주성분 축들 개수만큼의 차원으로 축소되어 표현된다. 간단한 Python sklearn 패키지에서 주성분 분석(PCA) 를 통한 차원 축소 예제를 구현해보자.
이전 챕터들에서도 많이 사용된 iris 데이터셋을 예제 데이터로 사용한다.
In[1]:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# iris 예제 데이터 로드
iris = sns.load_dataset('iris')
iris.head()Out[1]:
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosa
In[2]:
iris.info()Out[2]:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal_length 150 non-null float64
1 sepal_width 150 non-null float64
2 petal_length 150 non-null float64
3 petal_width 150 non-null float64
4 species 150 non-null object
dtypes: float64(4), object(1)
memory usage: 6.0+ KB
iris 데이터셋은 꽃잎(petal)의 길이와 넓이, 꽃받침(sepal) 길이와 넓이, 그리고 꽃 종류 총 5가지 특성으로 구성된다는 점을 알 수 있다.
In[3]:
sns.pairplot(iris, hue='species')Out[3]:
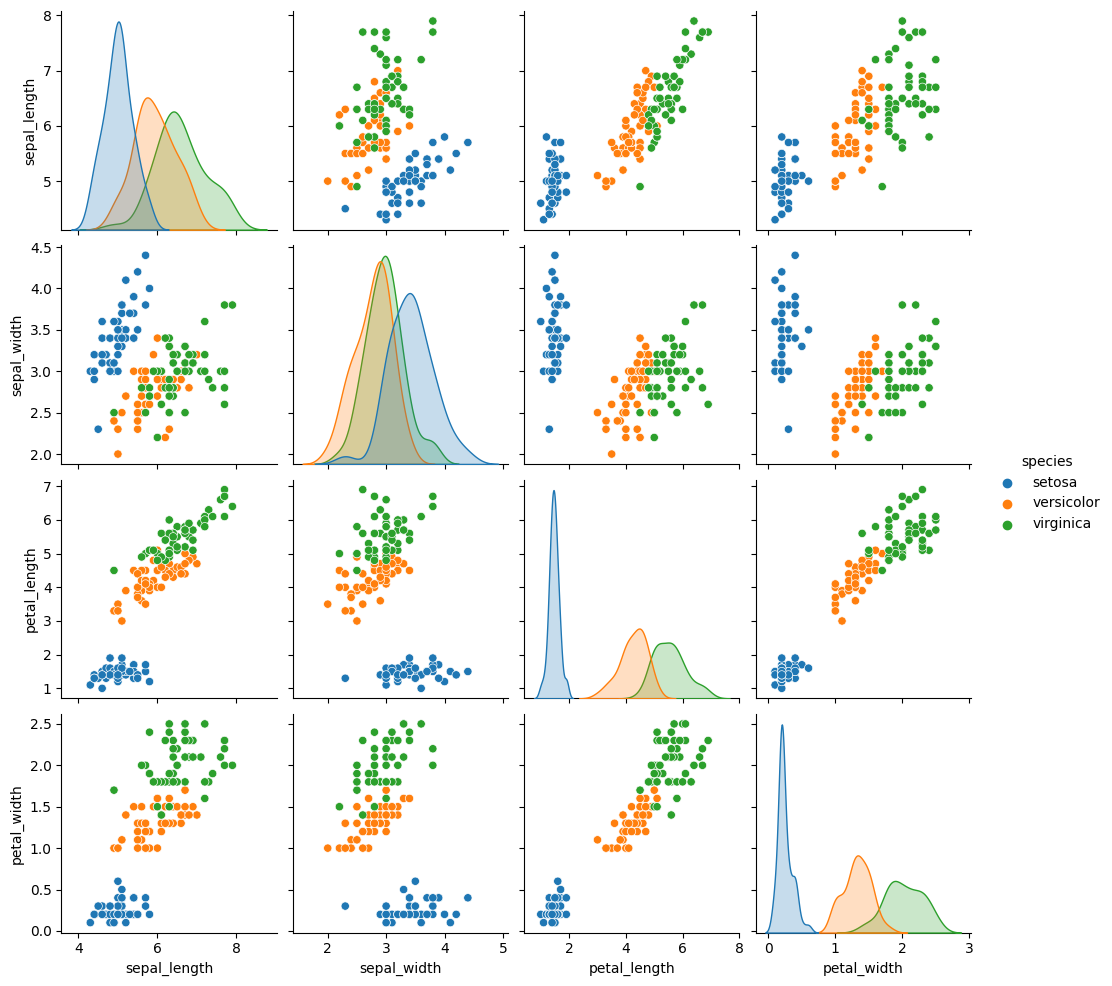
위의 시각화 그림을 분석해보자.
꽃의 종류(species)는 4개의 특성(sepal_length, sepal_width, petal_length, petal_width) 에 따라 표현될 수 있다. 4개의 특성을 모두 반영하여 하나의 공간에 표현하는 것은 인간이 시각적 이해하기 어렵고, 대신하여 2차원 공간에 데이터를 표현한다면 2개의 특성마다 꽃의 종류가 다르게 표현되는 모습을 볼 수있다.
In[4]:
# 모델링
columns = iris.columns
scaler = StandardScaler()
scaled_iris = scaler.fit_transform(iris[columns[:-1]])
pca = PCA(n_components=2) # 주성분 축의 개수 n_components
pca_iris = pca.fit_transform(scaled_iris)
df = pd.DataFrame(pca_iris, columns=['c1', 'c2'])
df['species'] = iris.species
dfOut[4]:
c1 c2 species
0 -2.264703 0.480027 setosa
1 -2.080961 -0.674134 setosa
2 -2.364229 -0.341908 setosa
3 -2.299384 -0.597395 setosa
4 -2.389842 0.646835 setosa
... ... ... ...
145 1.870503 0.386966 virginica
146 1.564580 -0.896687 virginica
147 1.521170 0.269069 virginica
148 1.372788 1.011254 virginica
149 0.960656 -0.024332 virginica
150 rows × 3 columns
주성분 분석 PCA (n_components=2) 의 결과로 label column인 species를 제외하고 기존 4개의 특성 (꽃잎 길이와 넓이, 꽃받침 길이와 넓이) 에서 c1 축, c2 축 2개의 특성으로 차원이 축소된 모습이다.
In[5]:
# 시각화
setosa = df[df['species']=='setosa']
versicolor = df[df['species']=='versicolor']
virginica = df[df['species']=='virginica']
plt.scatter(setosa['c1'], setosa['c2'], marker='o', color='b', label='setosa')
plt.scatter(versicolor['c1'], versicolor['c2'], marker='x', color='g', label='versicolor')
plt.scatter(virginica['c1'], virginica['c2'], marker='v', color='k', label='virginica')
plt.title('iris PCA')
plt.legend()
plt.show()
Out[5]:

PCA 결과로 2차원으로 축소된 iris 데이터의 분포이다.
'setosa' 꽃을 의미하는 파란색 동그라미 데이터는 완벽히 독립적으로 분류된 모습을 확인할 수 있으며, 나머지 두 꽃은 완벽히 분류되지는 않았지만, 일부를 제외하고는 적절히 분류된 모습을 확인할 수 있다.
지금까지 설명한 주성분 분석은 차원을 축소하는 방법들 중 하나의 종류이다.
이는 결코 n개의 Feature 를 가지는 데이터에서 특정 Feature 를 선별하는 Feature Selection 또는 Feature engineering 과는 의미가 다른 것임을 알아야한다.
때문에 PCA 를 통한 차원 축소를 통해 학습 속도 향상, 모델링 연산의 효율성 등을 기대할 수 있겠지만 근본적인 모델링 결과의 퍼포먼스를 향상시키는 것은 아니라는 점을 인지해야한다.
기타 차원 축소 기법들
일반적인 주성분 분석 이외에도 여러 차원 축소 방법들이 존재한다. 커널(Kernel)이라는 비선형 데이터를 고차원 공간으로 매핑하는 수학적 기법을 활용하여 비선형 데이터에 적용한 커널 PCA라는 방법이 있으며, 지역 선형 임베딩(LLE), 선형 판별 분석(LDA), MDS, lsomap, t-SNE 등 다양한 방법들이 존재한다. 사용 목적에 맞는 적절한 기법을 참고하는 것이 중요하다.
* 이미지 출처:
https://bioinformaticsandme.tistory.com/197
https://en.wikipedia.org/wiki/Principal_component
https://en.wikipedia.org/wiki/Projection_(linear_algebra)
글 | AI기술연구2팀 유용빈

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 3-8. 비지도 학습 (0) | 2023.07.26 |
|---|---|
| Chapter 3-7. GAM 이론 및 실습 (0) | 2023.06.29 |
| Chapter 3-5. 서포트 벡터 머신 (Support Vector Machine) (0) | 2023.04.27 |
| Chapter 3-4. 앙상블과 랜덤 포레스트 (0) | 2023.03.30 |
| Chapter 3-3. 결정 트리 (0) | 2023.02.22 |





댓글